If You Know a Percentage of a Number How to Figure Out the Remainder

What does per cent hateful?

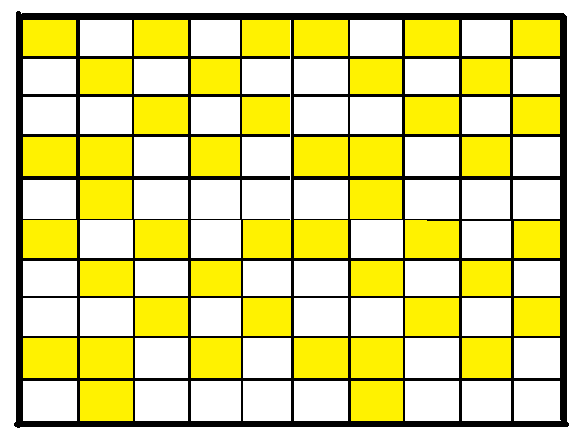
Look at the given foursquare. It is divided into 100 smaller squares. The shaded squares will always be a fraction of 100.  In that location are 44 shaded modest squares in this square. 44 out of 100 are shaded. You lot can also say that 44/100 is shaded.  You can as well say that 44 squares per hundred are shaded. When a fraction has 100 as the denominator, we call it a pct. 44/100 can be called 44 per cent. Per cent ways per hundred, every bit cent ways hundred. You can say that 44 per cent of the squares are shaded.

For per cent, nosotros apply the symbol "%". Thus 44 per cent volition be written as 44%.

In simple words, percentages are numerators of fractions with denominators 100. The per centum is also used to compare results.

Examples

Express each of the following as a percentage

Finding Per cent of a number

To detect the per cent of a number, nosotros write the per cent every bit a fraction with denominator 100 and so multiply by the number.

Example 1

Find 75% of 20

Solution

75% of twenty

 = (75/100)  x twenty

 = fifteen

Example ii

Observe 5% of £300

Solution

five% of £300

= (v/100) x 300

= £15

Writing per cent as a Decimal

In the starting time footstep, write the per cent as a fraction with the denominator 100.

And then, write the fraction as a decimal.

Example

Write each per cent as a decimal.

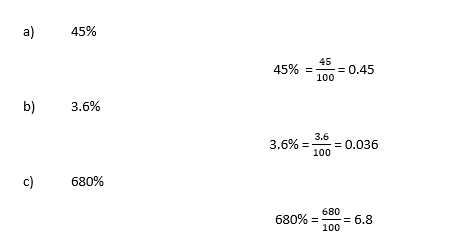
Comparison of Results using Percentage

Suppose, Henry scored 240 marks out of 300 and Peter scored 210 marks out of 250. Whose functioning is better or what is the percentage of marks scored by them?

Solution

To compare, first put the marks in the form of a fraction, i.east. 240/300 or 210/250 respectively.

Now discover the percentage of marks by multiplying the numerator and the denominator each by 100 as per cent means out of 100.

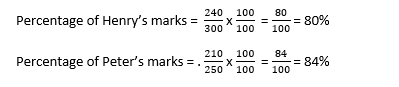
As Peter's percentage is more than Henry's, his performance is ameliorate.

Everyday Life Problems Involving Utilise of Percentage

Example 1

There are 600 students in a school. sixty% are boys. How many girl students are there in the school?

Solution

If sixty% are boys in the schoolhouse, then 40% are girls.

60% of 600 = (60/100) x 600 = 60 x half dozen = 360

Therefore, number of boys in the school = 360

And

Number of girls in the school = 600 – 360 = 240

Example ii

Silvia had 24 pages to write. By the evening, she had completed 25% of her work. How many pages were left?

Solution

Silvia had completed 25% of 24 pages by the evening.

Number of pages that were left = 75% of 24

 = (75/100) x 24

 = 18

Hence, eighteen pages were left to be written.

Case 3

The regular price of a computer was £25,500. Alice bought information technology from an online shopping site, which was selling it at a xx% discount on the regular cost. How much discount did Alice get? How much did she pay for the reckoner?

Solution

Regular cost of notebook computer = £25,500

Discount = xx% of £25,500

 = (xx/100) x £25,500

 = £5100

Amount paid past Alice = Regular Cost – Discount

 = £25,500 – £v,100

= £20,400

Hence Alice paid £20,400 for the estimator.

Example 4

Jack earns £12000 per month. Out of this, he spends 60% of food and other items of daily need, x% on rent and 5% on petrol for his scooter. How much does he save every calendar month?

Solution

Amount spent on food and other items = £(sixty% of 12000)

                                                                                = £(60/100  10 12000)

                                                                                 = £(60 x 120)

                                                                                 = £7200

Rent paid = £(10% of £12000) = £x/100  x 12000 = £(10 x 120) = £1200

Amount spent of petrol = £(5% of 12000)

                                                = £(5/100  x 12000) = £(v x 120) = £600

Total monthly expenses = £(7200 + 1200 + 600)

                                                 = £9000

Hence, his saving every month = £12000 – £9000 = £3000

Therefore, Jack saves £3000 every month.

Converting a Fraction or a Ratio into a Percentage

Ratios when expressed every bit fractions tin have different denominators in their simplest form. to compare them first of all, a common denominator is needed. The comparison becomes more than convenient if the denominator is 100. This implies that ratios are being converted into percentages.

Case

In a course of 50 students, the ratio of the number of boys to the number of girls is three: ii. Find the per centum of boys and girls in the grade.

Solution

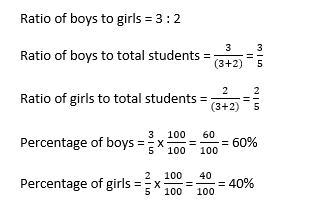
Unitary Method

The word unitary is derived from the give-and-take "unit" which means "one.

A unitary method is a method in which the value of a unit quantity is first derived to notice the value of any required quantity. In solving bug through the unitary method, two different things are compared as explained below:

1. When the total cost is compared with the number of items purchased, price per item is obtained.
2. When the distance traveled is compared with the total fourth dimension, the distance traveled per unit of measurement time is obtained.

Example

A train travels 1000 km in 5 hours. Find the percentage of altitude travelled by train in 3 hours.

Solution

The distance travelled by a train in v hours  = g km

The distance travelled past the train in 1 60 minutes = thou/5 km = 200 km

The altitude travelled past the railroad train in 3 hours = 200 km ten three = 600 km

Percentage = 600/1000 x 100 = 60%

A graphical representation of computing percentages has been presented below for amend agreement.

The guidance below will assistance you lot piece of work through percentage calculation problems including those constitute on the percent worksheets page.

Equally you guide your child you should also take the opportunity to explain the importance and relevance of percentage calculations: pay rises, allowance rises, interest rates, discounts on sale items etc. Learning is always improved when the relevance of what is being learned is appreciated.

What is a percentage?

Percent means "for every 100" or "out of 100." The (%) symbol as a quick way to write a fraction with a denominator of 100. As an instance, instead of saying "it rained 14 days out of every 100," we say "it rained 14% of the time."

Percentages tin can be written as decimals by moving the decimal betoken two places to the left:

Decimals can exist written as a percentages by moving the decimal point ii places to the correct:

Formula for calculating percentages

The formulas for computing percentages or for converting from percentages are relatively unproblematic.

To convert a fraction or decimal to a per centum, multiply by 100:

To convert a percent to a fraction, divide by 100 and reduce the fraction (if possible):

Examples of percentage calculations

The post-obit two examples show how to calculate percentages.

1) 12 people out of a full of 25 were female. What percentage were female person?

2) The price of a $ane.50 candy bar is increased past 20%. What was the new price?

3) The tax on an detail is $6.00. The tax rate is fifteen%. What is the price without tax?

Similar types of problems to those in the examples to a higher place are solved in a series of 3 mini-lessons onCalculating with Percent. These are listed below.

 #ane: Introduction

 #2: Calculating with Percent e.thousand. 12% of 80 is?

 #iii: Calculating with Per centum e.thousand. half dozen out of 8 is what % and 15 is 30% of what?

Percentage Chart

This Percentage Chart shows what fifteen% of $1 through $100 is although it is customizable and so yous tin set up the percentage and the numbers to whatsoever you want.

Find 1% – The Unitary Method

Handy Tip: A good way of finding percentages is to start by finding what 1% is.Instance: What is 6% of 31?

Observe 1%. Split by 100 (or move the decimal point ii places to the left)	31 ÷ 100 = .31
We now know what ane% is. Nosotros just demand to multiply it by 6 to observe 6%	.31 x 6 = 1.86

6% of 31 is 1.86

You can practise calculating percentages by get-go finding one% (and/ or finding 10%) and and so multiplying to get your last respond using this Calculating Percentages in Two Steps Worksheet. In that location are likewise more percentage worksheets here too.

Common mistake when finding a pct

Since percentages are often thought of as parts of a larger whole affair, there can be a tendency to carve up instead of multiply when faced with a problem such as "find 35% of 80." Equally the example below shows, after converting the percent to a decimal, the side by side step is to multiply, not divide.

An understanding of per centum allows students to guess to bank check whether their answer is reasonable. In this example, knowing that 35% is between ane-quarter and i-half would mean the answer should be somewhere between 20 and 40.

Recommended Worksheets

Percents and Discounts (Thanksgiving Themed) Math Worksheets
Applying Percentage, Base of operations, and Rate 6th Grade Math Worksheets

We spend a lot of time researching and compiling the information on this site. If you find this useful in your research, please use the tool below to properly link to or reference Helping with Math as the source. We capeesh your back up!

muellerraingerred.blogspot.com

Source: https://helpingwithmath.com/calculating-percentages/

Share this post